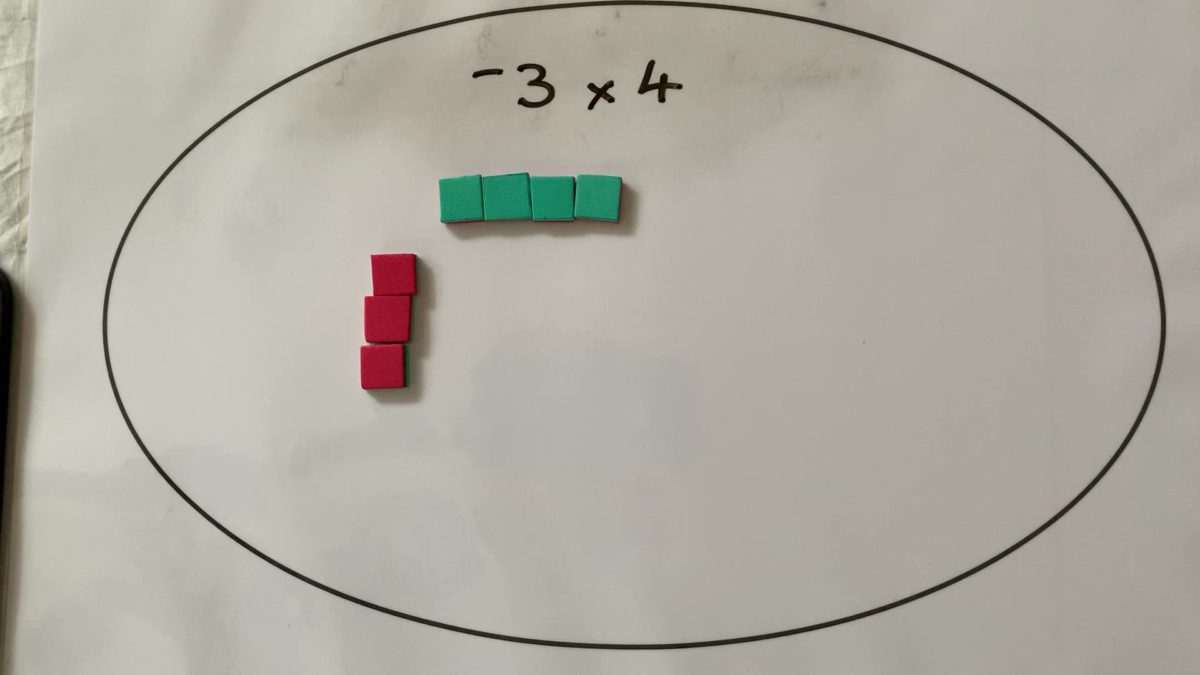Tag: manipulative

Algebra Tiles Part 1 – The wonderful manipulative you have never used?!

In this blog, the first of a series, I will show you Algebra Tiles – how to make them and how to introduce them to your students.

This is the first part of a series of blogs on Algebra Tiles. In Part 1 of this blog series, I will be focussing on introducing Algebra Tiles to your students, making your own Algebra Tiles, and using Algebra Tiles to model the four operations with integers.

Although not part of this blog readers should be aware of the Concrete Representation Abstract Model (CRA). In this model, it is suggested that students move through a series of stages when learning a new concept. Students first experience a concept using concrete objects or manipulatives, they then draw diagrams or representations of the concepts and finally move towards the use of abstract symbols. I will be referencing this model throughout this blog series. For more information on this see the Padlet I have made to accompany this blog series.

What are Algebra Tiles?

In this video clip I introduce the three tiles and what they represent.

Why make your own Algebra Tiles?

There are many commercially available Algebra Tiles, but I like to make them with the students. This is for a number of reasons:

  • The students will then feel that they “own” their tiles.
  • The process of measuring and cutting can tell you a lot about your students’ skills (or lack thereof)
  • The students can pick their colours – this is especially important for students with visual impairments

Here is the template I used for making my tiles and here is the template for the baseboard that I use in the videos.

To make the tiles:

  • Stick two A4 sheets of foam together, this is easiest if one of the sheets has a sticky back.
  • Then rule the sheet according to the template or use the measurements below:
    • unit squares were 1.5cm x 1.5 cm
    • variable rectangles were 1.5cm x 7cm
    • variable squared squares were 7cm x 7cm
  • Cut the shapes using a craft knife as scissors will pull the foam.
  • Keep the tiles in a resealable bag

You might also want to give the students a laminated A3 sheet to work on, so they can annotate and write notes as they use the tiles.

Using the unit tile to model the four operations

In this video clip, I show how the unit tile can be used to model integer addition and the meaning of a zero-sum pair. This concept is key to using Algebra Tiles.

The following clips demonstrate how Algebra Tiles can be used to model the other operations, subtraction, multiplication and division and directed numbers.

Subtraction of directed integers

Another example of subtraction with directed integers

Using the array model for multiplication

Using the array model and Algebra Tiles for multiplication of directed integers

Using the array model and Algebra Tiles to model division

Points to think about as you watch the video clips:

Using manipulatives in older year levels

It is rare to see manipulatives being used in a high school classroom. It is even rare to see them much beyond Year 3! The impression students have is that using manipulatives is infantile and only for those that are struggling. This is not the case and many (all?) students would benefit from using them, even if only for a short period.

I like to give the students time to familiarise themselves with the manipulative before I explain how we will be using them. I will ask the students to think about how they think the manipulative could be used, what mathematics it might be used with.

I might say to teachers that I “allow the students time to ‘play’ with the manipulative”, but I would be careful with the use of the term ‘play’ with students, as students should not view manipulatives as toys, as this would only reinforce the notion that they are not a serious tool for the exploration of mathematical concepts.

The language one uses

When using the tiles, be aware of the language you use. It is easy to use the same term for multiple concepts.

For instance, the word ‘minus’. Does this mean the operation subtraction or that the integer is a negative? How would you read the following?

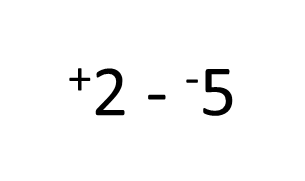
Would you say, “plus 2, minus, minus 5”? This can be very confusing for students. By being careful to use the terms positive and negative to indicate the direction of the integer only, and not plus and minus or similar, can help to prevent this confusion. For this example, it would be better to say, “positive two, subtract, negative two”.

Giving the positive integer a direction is important. All integers have a direction. As mathematicians tend to be lazy, we drop the term positive as most numbers we deal with are positive. Students need to understand this point.

Give students plenty of time to use the manipulative

Give the students plenty of time to use the tiles. There will be students that ‘get’ the concepts very quickly and will feel that the tiles are not necessary. I would encourage the students to use the tiles a few times at least. Ask the students to record their thinking by taking photos or drawing pictures/diagrams of what they are doing (the R in the CRA model).

Remember the CRA model does not describe a linear process. Students should feel comfortable in picking up and using the manipulative anytime they feel that would be useful. The manipulatives should, therefore, be readily available and accessible.

Comments

Please use the comment section to let me know if you found this introduction to Algebra Tiles useful and, if you used them with your students, how that went.

In Part 2 of this series, I will show how Algebra Tiles can be used to build algebraic expressions, used to model the addition and subtraction of algebraic expressions, and used to model substitution into algebraic expressions.

Virtual manipulatives – An exciting way to visualise maths

During the COVID-19 pandemic the educational world has under gone a huge change and shift in thinking. Many teachers have had to look for new ways to deliver concepts in maths. From the increase in activity and membership I have seen on my Facebook site there has been a renewed interest in the use of manipulatives when teaching mathematics. Using online, virtual manipulatives has given:
  • students a new way of thinking about and visualising maths
  • teachers a new way of presenting concepts
There are many students that have thrived in this new learning environment. In discussions I have had with teachers, maths seems to have been the subject where most students have made good progress while learning online. Even those students that generally struggled in the classroom. The lack of distractions  the, often, smaller teaching groups and more focussed attention they have received has proved to be beneficial. I am a great believer and proponent of using concrete materials. The physical experience of touching and moving manipulatives while learning maths is an excellent way to fix ideas and concepts. During the move to online learning many teachers had to look for new ways to deliver the concepts they have been teaching for years. In their search they have discovered the myriad of virtual manipulatives that are available. Many teachers are using manipulatives more now than they did in their physical classrooms. When we return to the classroom ideally we should switch to the physical manipulative, and  not just continue with the virtual. The virtual manipulative is certainly better than no manipulative, but I do not believe that it can replace the physical. The ability to make this switch will depend on the availability of concrete materials and budgetary constraints. Teachers should be looking in cupboards for those dusty Cuisenaire rods and searching for those long forgotten resources that are hiding in so many schools. Let us all use the amazing teaching and learning that we have been doing online and transfer to the classroom with the resolve to keep looking for innovative and creative ways to deliver the maths curriculum and to foster creativity and growth in our students. My situation has changed too. I am no longer working in a school and must think about what is next. I am looking to start a maths education consultancy. Taking the ideas of growth mindset in maths and the use of manipulatives to schools, students and parents. Still working on the idea. Look out for the launch in the coming weeks.

Numerule: A teacher’s review of the innovative maths tool

This year I was lucky enough to present at a few mathematics conferences. At two of them, MAWA (Mathematical Association of Western Australia) and MAV (Mathematical Association of Victoria) I presented on the topic of ‘Using Manipulatives in the High School Classroom’. I had a great response to this topic with all the presentations well attended and really good discussions.

I realised that this was a topic that teachers were interested in and I began to think of ways to continue and grow the discussion. In a moment of madness, I started the FaceBook page Maths Manipulatives and was amazed at the response. I had 50 members in 10 minutes and a request to review a product. By the end of 48 hours, I had 1400 group members and the number has been slowly growing since then.

In this post, I will be reviewing the Numerule. I first saw this at the MAV conference and thought that it looked like a clever idea. 

What is a Numerule?

The Numerule is a 30cm ruler that doubles as a simple counting tool for use in Lower Primary classrooms. Corresponding to each number on the ruler is a ‘button’ that can be pressed. Once pressed the button stays down, pushing up from underneath returns it to its original state. The buttons are grouped in tens by colour (blue, white and red).

The information that comes with the Numerule describes how it can be used for the four operations as well as for recording data. There are videos on the website showing children performing these tasks. The information also includes links to many Australian Curriculum descriptors. The website also has a teacher’s notes to download.

Trying it for the first time

As I received the Numerule, after school had finished I brought it to try out with my 6-year-old granddaughter. I gave it to her to look at without telling her what it was. She immediately started to push the buttons and saw that they could be pushed back into position. She used the ruler to measure a few things and told me that it could be used to draw straight lines. I asked her about the buttons she told me that they were in groups of ten and then counted in tens to 30.

I then told her that we could use it to do some maths questions. I asked her to show me how she could do 6 plus 5. She thought for a bit and then pushed down the 6 and counted on five, pushing the buttons as she went. The answer she told me was 11. I was impressed at how intuitive she found using it. We tried a couple more questions and she enjoyed doing them. 

She then said look – and pushed down every other button and showed me that this was counting in two’s. Again this was without prompting.

I then guided her a little and we looked at subtraction problems. She then took the Numerule to bed!

My impression of the Numerule

Having now seen the Numerule in action I can see that it is a good design and looks to be strong enough to last in the classroom. My granddaughter took to it and quickly saw how to use it. I can see that in the classroom this could be a useful tool. As every student should have a ruler having one that doubles as a calculation aid makes sense.

If I have any criticism it would be that for the age group it is aimed at I would have grouped the colours in fives, not tens. This is how I make bead strings with students. I like the tactile nature of pressing the buttons and the way it can be used for data collection and representation. 

Also, it is a little pricey at $14 (15% less if you buy over 25) but I was told that it is virtually unbreakable so should last. My younger grandchildren had a go with it and it did stand up to some quite rough treatment.