In this, the last post of the Algebra Tiles series, I will be looking at how you can use the tiles to demonstrate various more advanced ideas, such as the difference of two squares and completing the square.
Dividing a quadratic expression by a linear factor
Dividing a quadratic expression by a given linear factor is similar to factorising. Doing this is the same as for factorising, you are building a rectangle, but one of the side lengths is now fixed.
Here are three examples of such divisions in increasing complexity:
Perfect Squares
What is a perfect square? The result of multiplying two identical linear expressions! So we are building squares, not rectangles.
You can use the visual representation to discuss the features of a perfect square and how to recognise one when written out in full:
(x + 3)2 = (x + 3)(x + 3) = x2 + 6x + 9
Difference of Two Squares
By showing students a visual representation and using the tiles to demonstrate the addition of zero-sum pairs, students should be able to see the pattern formed when factorising the difference of two squares.
Completing the Square
What do we mean when we talk about ‘completing the square’?
By attempting to build a square, with the given expression, and showing that we may need to add or remove terms to achieve the square, we can make meaning of the term ‘completing the square’. In the second video, I show how you may need to add in zero-sum pairs to complete the square.
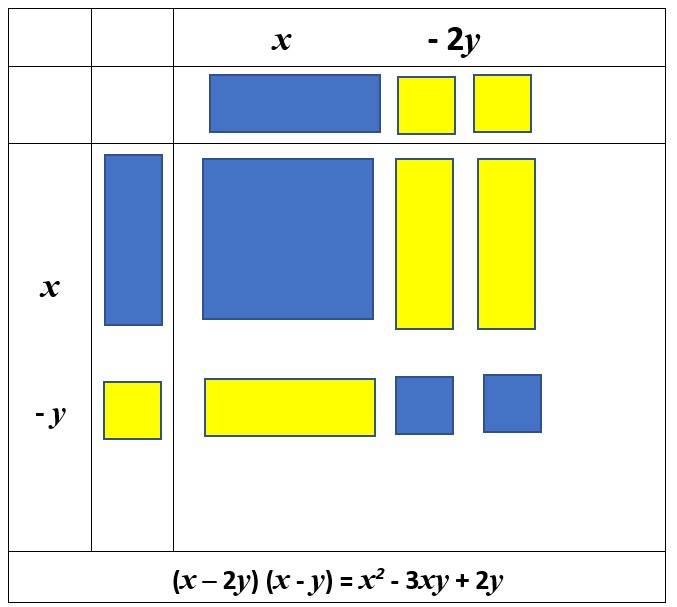
Extending to Two – Variables
I did mention when talking about collecting like-terms, in Part 2 of this series, that you can model expressions that contain two-variables. In this video I show how to do that:
Resources
There is a Padlet to accompany this blog series with links to research, virtual manipulatives and other resources.
Thank you for following this blog series.